Suffix Trees , a bit complicated but really powerful data structure

Continuing with my obsession with the string matching algorithms , after 
KMP algorithm which does string matching in O(n +k) time , where n is length of the string and k is the length of the pattern. I tried exploring another data structure called as “Suffix Trees” , Suffix trees are nothing but compressed tries , where you model all the suffix present in a string in an optimized tree/trie structure.

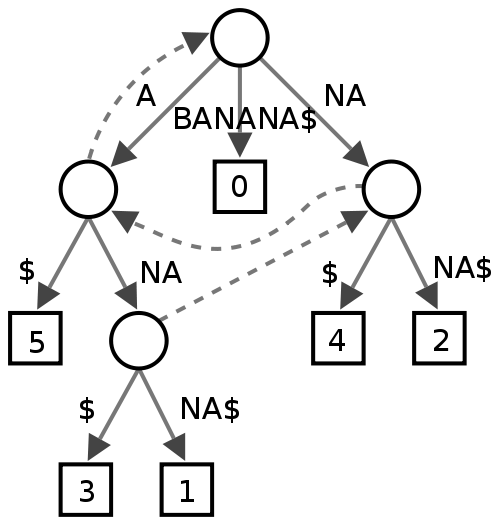
this is how a suffix tree for word “BANANA” will look like

some of the other common use cases , where suffix trees can be used is 

• Find the longest common substring of the strings S and T. This can be done in time O(|S| + |T|)


• 
  

  Find the longest substring of S that appears at least m > 1 times. This query can be answered in O(|S|) time.

  
  

Traverse the suffix tree labeling the branch nodes with the sum of the label lengths from the root and also with the number of information nodes in the subtrie.

Traverse the suffix tree visiting branch nodes with information node count >= m. Determine the visited branch node with longest label length.

• Find all strings that contain a pattern P. Suppose we have a collection S1, S2, … Sk of strings and we wish to report all strings that contain a query pattern P. For example, the genome databank contains tens of thousands of strings, and when a researcher submits a query string, we are to report all databank strings that contain the query string. To answer queries of this type efficiently, we set up a compressed trie (we may call this a multiple string suffix tree) that contains the suffixes of the string S1$S2$…$Sk#, where $ and # are two different digits that do not appear in any of the strings S1, S2, …, Sk. In each node of the suffix tree, we keep a list of all strings Si that are the start point of a suffix represented by an information node in that subtrie.

i have referred to http://stackoverflow.com/questions/9452701/ukkonens-suffix-tree-algorithm-in-plain-english/22126672#22126672

to write an implementation for the suffix trees , the above link explains it very nicely on how to build your own suffix trees.